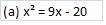Bab 3 - SET - (CONTOH 15 - CONTOH 16)

CONTOH 15

Diberi semester, Є = {4, 8, 12, 16, 20} dan Y = {12, 20}. Senaraikan Y' dan lukiskan gambar rajah Venn untuk mewakilinya.

Penyelesaian
Y' = {4, 8, 16}

CONTOH 16

Gambar rajah Venn dalam Rajah 3.13 menunjukkan set semester, (E), set P, Q, dan R.

(a) Senaraikan semua unsur bagi (i) ε (ii) P (iii) R'
(b) Tuliskan satu hubungan di antara ε, P dan Q.
(c) Lukiskan gambar rajah Venn untuk mewakili bilangan unsur dalam set semesta, E, set P, Q dan R.

Penyelesaian
(a) (i) ε = {1, 2, 3, 4, 5, 6, 7, 8}
     (ii) P = {1, 2, 4, 6, 7}                    Termasuk unsur set Q kerana Q C P
    (iii) R' = {1, 2, 3, 4, 6, 7}               Unsur di luar R tetapi di dalam E

(b) Q C P C ε                       Semua set adalah subset bagi  set semesta.   

(c) 

CONTOH RESUME

Bab 3 - SET - (CONTOH 13 - CONTOH 14)

CONTOH 13

Diberi SEMESTER, ε ; {nombor bulat yang kurang daripada 8}
                               M = {nombor ganjil} dan N = {faktor bagi 18}

Lukiskan gambar rajah Venn untuk menunjukkan hubungan di antara

(a) ε dengan M
(b) ε dengan N

Penyelesaian

ε = {0, 1, 2, 3, 4, 5, 6, 7}
M = {1, 3, 5, 7}
N = {1, 2, 3, 6}

(a) & (b)

CONTOH 14

(a) Diberi ε = { x : 11 < x < 20, x integer} dan

               R = {nombor perdana}. Nyatakan set pelengkap bagi R.

(b) Diberi ε = {huruf abjad dalam perkataan "HORMAT" dan

                S = {huruf konsonan}. Senaraikan semua unsur dalam S'

Penyelesaian

(a) R = {11, 13, 17, 19}

maka, R' = {12, 14, 15, 16, 18, 20}

(b) S = {H, R, M, T}

maka, S' = {O, A}

INFO:

Bab 3 - SET - (CONTOH 7 - CONTOH 12)

Contoh 7

Diberi A = {faktor bagi 24} dan B = {x : 10 < x < 30, x integer}. Carikan nilai n(A) dan n(B).

Penyelesaian

A = {1, 2, 3, 4, 6, 8, 12, 24}
Maka, n(A) = 8

B = {10, 11, 12, ..., 30}
Maka, n(B) = 21

INFO:

Contoh 8

Tentukan sama ada setiap set yang berikut adalah set kosong atau bukan.

(a) M = {logam dalam keadaan cecair pada suhu bilik}

(b) N = {nombor perdana yang terletak di antara 23 dan 29}

Penyelesaian

(a) M = {merkuri}

M bukan set kosong, iaitu M     

(b) N adalah set kosong, iaitu N =          24, 25, 26, 27 dan 28 bukan nombor perdana

Contoh 9

Tentukan sama ada setiap pasangan set berikut adalah set sama atau bukan.

(a) A = {a, b, c}, B = {a, b, c, d}
(b) G = {k, i, p, a, s}, H = {s, i, k, a, p}
(c) P = {1, 2, 3, 6}, Q = {faktor bagi 6}

Penyelesaian

(a) A B            Set A tidak mempunyai unsur d
(b) G = H                 Set G dan set H mempunyai unsur yang sama
(c) P = Q                 Q = {1, 2, 3, 6}, maka unsur-unsur dalam set P dan set Q adalah sama


Contoh 10

Diberi J = {1, 2, 3, ..., 9}, K = {5, 6, 7, 8} dan L = {7, 8, 9}. Nyatakan sama ada setiap yang berikut benar atau palsu.

(a) K C J
(b) L C K
(c) L C J

Penyelesaian

(a) Benar        Setiap unsur K terdapat di dalam J
(b) Palsu         9 tidak terdapat di dalam K
(c) Palsu         L adalah subset bagi J

Contoh 11

Tunjukkan hubungan pasangan set berikut dengan menggunakan gambar rajah Venn.

(a) P = {a, b, c, d, e, f, g}, Q = {c, e, g}
(b) R = {ahli Persatuan Matematik Sekolah Menengah Taman Seroja}
     S = {pelajar Sekolah Menengah Taman Seroja}

Penyelesaian

(a) & (b)

Nama pelajar terlalu banyak, maka unsur-unsurnya tidak perlu ditulis dalam gambar rajah Venn.

Set itu sendiri dan set kosong juga adalah subset bagi suatu set. Set kosong adalah subset bagi semua set.


Contoh 12

Nyatakan semua subset yang mungkin bagi

(a) {a, b}
(b) {1, 2, 3}

Penyelesaian

(a) O, {a}, {b}, {a, b}

(b) O, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}

Bab 3 - SET - (CONTOH 5 - CONTOH 6)

CONTOH 5

Lukiskan gambar rajah Venn untuk mewakili set berikut:

(b) X = {5, 10, 15}

(c) Y = {huruf abjad dalam perkataan "PEMIMPIN"}


Penyelesaian

(b) & (c)

Y = {P, E, M, I, N}

CONTOH 6

Diberi X = {huruf abjad dalam perkataan "AMANAH"}, carikan nilai n(X).

Penyelesaian

X = {A, M, N, H}              Unsur yang sama tidak perlu diulangi       

Maka, n(X) = 4

Bab 3 - SET - (CONTOH 1 - CONTOH 4)

CONTOH 1 Senaraikan unsur - unsur setiap set berikut dalam tanda kurung  {    }.
(a) set A ialah set huruf - huruf konsonan dalam perkataan "GIGIH"
(b) B = {nombor ganjil yang kurang daripada 10}
(c ) C ={x : 10 < x < 20, x integer genap}

Penyelesaian

(a) A = {G, H}            Unsur yang sama tidak perlu diulangi

(b) B = {1, 3, 5, 7, 9}

(c ) C = {10, 12, 14, 16, 18, 20}

CONTOH 2

Tulis setiap set berikut dengan menggunakan perihalan.

(a) R = {Melayu, Cina, India}

(b) S = {2, 3, 5, 7}

Penyelesaian

(a) R ialah set kaum-kaum utama di Malaysia

(b) S ialah set nombor perdana kurang daripada 10.


CONTOH 3

Diberi P = {poligon sekata}

Tentukan sama ada setiap yang berikut merupakan unsur bagi set P atau bukan.

(a) kubus
(b) rombus
(c) lelayang

Penyelesaian

(a) Kubus bukan unsur bagi set P.          Kubus mempunyai isipadu, iaitu dalam bentuk tiga matra
(b) Rombus adalah unsur bagi set P.      Panjang keempat - empat sisi rombus adalah sama
(c ) Lelayang bukan unsur bagi set P.     Panjang sepasang sisi lelayang adalah berbeza daripada
                                                             panjang pasangan sisi yang lain.

INFO:

CONTOH 4

Diberi A = {faktor bagi 30}, B = {empat gandaan 5 yang pertama} dan
C = {nombor perdana yang kurang daripada 15}. Lengkapkan setiap yang berikut
dengan menggunakan simbol
atau Є

(a) 15 ?  A

(b) 25 ? B

(c) 2 ? C

(d) 17 ? C

Penyelesaian

A = {1, 2, 3, 5, 6, 10, 15, 30}
B = {5, 10, 15, 20}
C = {2, 3, 5, 7, 11, 13}

(a) 15  Є  A              15 adalah unsur bagi A

(b) 25 B         25 bukan unsur bagi B

(c) 2  Є C               2 adalah unsur bagi C

(d) 17  C      17 bukan unsur bagi C

JAWAPAN LATIHAN PENGUKUHAN - BAB 2 - UNGKAPAN DAN PERSAMAAN KUADRATIK

Bab 3 - Set - Nota Ringkas

Latihan Pengukuhan

Bab 2 - Contoh 18

Sempena Hari Kebangsaan, suatu pesta laut telah diadakan. Acara yang berlangsung termasuk perlumbaan perahu naga dengan jarak perlumbaan 500 m. Kelajuan pasukan yang menjadi johan adalah 1 m s^-1 lebih cepat daripada kelajuan pasukan yang menjadi naib johan. Jika jumlah masa yang diambil oleh kedua-dua pasukan itu ialah 3 minit 45 saat, carikan kelajuan pasukan naib johan.

Penyelesaian

Bab 2 - Contoh 17

Selesaikan

(a) 

(b) 

Penyelesaian

Bab 2 - Contoh 16

Tentukan punca bagi persamaan kuadratik


Penyelesaian

Bab 2 - Contoh 15

Tentukan punca bagi persamaan kuadratik berikut dengan menggunakan kaedah cuba-cuba.

Penyelesaian

(a) dan (b)

Bagi persamaan kuadratik berbentuk x² + bx + c = 0, puncanya merupakan faktor
bagi c dan mungkin bernilai positif atau negatif.

Bab 2 - Contoh 14

Dengan cara penggantian, tentukan sama ada nilai anu yang diberi adalah punca persamaan kuadratik yang diberi atau bukan.


(a) 


(b) 


Penyelesaian

(a) & (b)

Bab 2 - Contoh 13

(a) Encik Johan merancang untuk membuka sebuah kafe internet. Diketahui bahawa setiap tempat duduk adalah berbentuk segi empat tepat, yang panjangnya 0.5m lebih daripada lebarnya. Jika Encik Johan ingin menyediakan 25 tempat duduk dalam kawasan yang luasnya 125 m2, bentukkan satu persamaan kudratik berdasarkan maklumat di atas.

(b) Kelajuan seorang penunggang basikal dari Bandar Melaka ke Tampin mengikut arah
angin adalah 6 km j^-1 lebih laju daripada kelajuan dari Tampin ke Bandar Melaka mengikut arah lawan angin. Jika jarak antar Bandar Melaka dan Tampin ialah 36 km dan beza masa yang diambil ialah 1 jam, bentukkan satu persamaan kuadratik berdasarkan maklumat ini.

Penyelesaian

(a)

   
   
   












(b)

Bab 2 - Contoh 12

Tulis semula setiap persamaan kuadratik yang berikut dalam bentuk am.

(a) 


(b) 


(c) 


Penyelesaian


(a)



(b)

INFO :

(c)

Bab 2 - Contoh 11

Nyatakan sama ada persamaan yang berikut adalah persamaan kuadratik dalam satu anu atau bukan.

(a) 

(b) 

(c) 

(d) 

(e) 

(f) 


Penyelesaian

(a) 

= adalah persamaan kuadratik dalam satu anu kerana hanya terdapat 1 anu,
y dan kuasa tertinggi bagi y ialah 2.
__________________________________________________

(b) 

Maka,   adalah persamaan kuadratik dalam satu anu

kerana hanya terdapat 1 anu, x dan kuasa tertinggi bagi x ialah 2.

__________________________________________________

(c)  bukan persamaan kuadratik dalam satu anu tetapi merupakan

ungkapan kuadratik.

Perhatikan bahawa tiada tanda kesamaan.

___________________________________________________

(d)  bukan persamaan kuadratik dalam satu anu kerana kuasa tertinggi bagi y ialah 3.
___________________________________________________

(e)  bukan persamaan kuadratik dalam satu anu kerana melibatkan

dua anu, x dan y.
____________________________________________________

(f)  bukan persamaan kuadratik dalam satu anu kerana kuasa

tertinggi bagi anu, k ialah 3.